Conjunction fallacy and “safety” in accumulator bets
Overloading a betting ticket with several ‘sure bets’ for the sake of ‘safety’ is an unwise strategy in sports betting. The bettor might overestimate the chances of those events happening together and as such, commit a conjunction fallacy when placing accumulator bets.
In sports betting there are two main general strategies that bettors may embrace:
- One is that of chasing surprise (which offers high payout odds) and placing a bet on such event, as an individual bet or combined with one or more other bets.
- The other is that of betting only on “almost sure” events (such as the victory of the top/strong teams), as a form of “safety”.
The latter strategy suits players who frequent £10 betting sites, looking for regular small profits rather than low-chance big hits. After all, the payout odds of such “sure” bets are low (1.1 – 1.5 to 1 as an average range). However, the effectiveness of such a “safe” or “defensive” strategy depends essentially on a subjective factor, that every bettor has to decide on before placing a bet, namely how many events they will choose for an accumulator bet.
If safety also assumes a low investment for the bettor, given the low payout odds of a “safe” bet, this will also imply a low possible profit. The only way to increase the possible profit is by making a combined bet with several such events, known as an accumulator or parlay wager.
In this article we shall discuss such “safety”, see how the number of events on the ticket may affect it, and draw conclusions about what this number should be for keeping the bet relatively safe.
Overloading the ticket in sports betting
Under the constraint of a fixed stake as investment and low payout odds, it is normal for a bettor to have the impulse of loading their ticket with several bets. These kind of accumulator bets are driven on the one hand, by the goal of having a higher payout than for one bet and, on the other hand by the belief that the chances for a win do not decrease greatly if betting on several “sure” events rather than a single event.
Let’s take a concrete example.
Imagine that the bettor chooses some matches where the prior information indicates a favorite to win (as such, their payout odds will be low) and decide to place an accumulator bet on those matches, by betting on the victory of the favorite teams.
Assume the bettor chose to bet on only four such matches on a ticket, each having 1.2 as payout odds:
Match 1: victory of the favorite team; ×1.2 payout odds
Match 2: victory of the favorite team; ×1.2 payout odds
Match 3: victory of the favorite team; ×1.2 payout odds
Match 4: victory of the favorite team; ×1.2 payout odds
Total (combined) odds: 1.2 × 1.2 × 1.2 × 1.2 = 2.07
Assume the bettor estimates (subjectively) a probability of 70% for any of those “safe” events, assumed independent of each other. Then the probability of their conjunction (the event that occurs if each of those four events occurs) is (70/100) × (70/100) × (70/100) × (70/100) = 24.1%. The chances decreased about three times in relation to the chances for a single match, and the decrease would be even higher with new matches added on that ticket. Probability is a subunitary number, and the product of any multiplication of probabilities would decrease with the number of factors. Hence, the “safety” induced by a high probability for one match is drastically reduced when increasing the number of matches on the ticket.
How probability decreases with large conjunctions of events
We saw in the previous section a concrete example of how probability decreases with multiplication, as being subunitary. To understand and perceive the reason of this decrease in general, we have to analyze it in its combinatorial nature. This decrease is the effect of the power of multiplication of combinations and can be illustrated through unfolding. In the following incomplete diagram, the possible result of each match (1 – victory of the hosts, X – draw, and 2 – victory of the guests) is combined with the possible results of the other matches as an unfolding of paths (each node stands for a match):
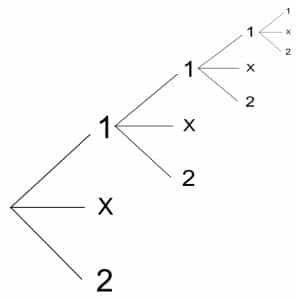
In total, there are 3×3×3×3 = 81 paths and only one out of them, say 1–1–1–1, corresponds to a good prediction for the four matches. In one single match, the good prediction would be one out of three. Of course, this diagram does not reflect the real chances, as the three possible results are not equally probable – in fact, the bettor assigned a 70% probability for the result 1 and the house also estimates this result as highly probable. If it were, the chances for a good prediction of a single match (1/3) would decrease to 1/81 in the combined bet.
We can reflect the assigned chances in the diagram by adding additional equally probable nodes and implicitly paths, in a certain proportion. For instance, assuming 70% chances for 1, 20% for X, and 10% for 2, the (incomplete) diagram would look like the one below, where each path is assigned a 10% chance:
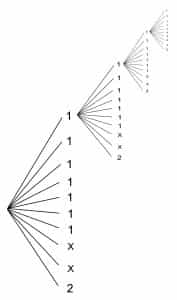
Counting now the number of paths favorable for the result 1–1–1–1, we find 7×7×7×7 = 2,401 out of a total of 10×10×10×10 = 10,000 possible paths. Doing the ratio, we get 24.01% as the probability of that result.
When faced with the proven decrease in chances, the bettor might be asked why they prefer not to place a bet with identical payout odds (about 2 : 1) on a different single event instead of that combined bet, provided that the chances estimated for that single bet are higher than those of 24.01%. If the bettor does not have a clear answer for that, they might overestimate the probability of the conjunction, influenced by the good chances of the favorite teams in those matches.
This overestimation falls within what psychologists call the conjunction fallacy.
Conjunction fallacy and how it affects sports betting
Roughly speaking the conjunction fallacy is an overestimation of the probability of a conjunction of events. If two events are independent to each other, the probability of their conjunction is the product of their individual probabilities: P(A and B) = P(A) x P(B). It follows directly that the probability of the conjunction is less than each individual probability, since probabilities are subunitary numbers. A particular form of the conjunction fallacy as a mathematical error is when the subject takes the probability of the conjunction to be the sum, instead of product, of the individual probabilities. In its usual form, the fallacy involves a false belief (based on a kind of “feeling”) that the probability of the conjunction is higher than the probability of an individual event within the conjunction. Cognitive psychologists think that the too-descriptive presentation of the measured events favours the fallacy.
Conjunction fallacy manifests in gambling, especially in those contexts that involve descriptive references of the measured events or in which the player accesses prior information associated with those events. Such conditions are usually found in sports betting, and this is why conjunction fallacy is more frequent in such games than in others.
For example:
Imagine a horse race where Horse 1 is the big favorite (say it won five out of the last seven races), and Horse 2 is an average horse with promising performance in the last races. Assume a bettor considers the following events for placing a bet on:
- Horse 1 wins;
- Horse 2 is the second;
- Horse 1 wins and Horse 2 is the second.
Assume the bettor is more concerned with the chances to win than with the payout odds for the three events. If the bettor believes that event 3 is more probable than one or both of the events 1 and 2 (and accordingly he places the combined bet 1 and 2 on the same ticket), the bettor is subject to conjunction fallacy, since event 3 is a conjunction of the other two events. This fallacy may turn into a loss for the bettor, as they could bet on events 1 and 2 on separate tickets, with higher chances each. But, they could win with that combined bet as well. The concept is; that the belief the betting decision was based on was incorrect.
Another kind of instance of conjunction fallacy in sports betting is the following:
In considering the bets associated with a match between teams A and B, the bettor evaluates the chances of the following bets:
- Team A scores one goal;
- Team B scores one goal;
- The final score of the match is 1 – 1.
If estimating the chances of bet 3 as higher than either of those of bets 1 or 2, the bettor commits a conjunction fallacy, since event 3 is the conjunction of the other two. Again, the prediction for 1 – 1 might come true, but that would not validate the wrong reason based on a comparison of chances.
We can associate our examples of overloading a ticket with “sure” events in the previous sections with a usual form of conjunction fallacy. The belief that the winning chances don’t change much with the number of matches in the combined bet is conjunction fallacy also.
Whatever the physiological factors favorizing conjunction fallacy, it is well known that in sports betting, players usually have an impulse to combine as many bets as possible on the same ticket, to a certain subjective limit, since the payout odds increase with multiplication. We already saw in the earlier sections that following this impulse is not wise, but how should we deal rationally with the “safe” combined bets in what concerns the number of bets on the ticket?
Splitting or collapsing the combined bet to keep it safe
Besides a possible conjunction fallacy, in terms of optimal play if safety is concerned, it is safer to split a ticket with “sure” or “almost sure” events and its stake. In our initial example, playing two tickets – holding two matches each – instead of one and halving the stake in two is safer. Assume S is the stake of the original ticket with four matches and S/2 the stake of each reduced ticket:
Ticket A, stake S/2:
Match 1: victory of the favorite team; ×1.2 payout odds
Match 2: victory of the favorite team; ×1.2 payout odds
Ticket B, stake S/2:
Match 3: victory of the favorite team; ×1.2 payout odds
Match 4: victory of the favorite team; ×1.2 payout odds
Each ticket has 1.44 : 1 payout odds. In case all four results are predicted well, the two winning tickets together give a profit of 0.44S (less the possible ticket fee charged by the agency; usually online agencies do not charge such fee), which, compared to the possible profit of the original unsplit ticket, namely 1.07S, is indeed lower. However, if one result is predicted wrongly, one of the tickets A and B loses, and the overall loss is (S/2) – 0.44×(S/2) = 0.28S, which is about three times lower than the possible loss with the initial ticket (S). If staying with the original ticket, it would be losing anyway in this situation.
Therefore, it is safer to split the ticket in two, which supports the idea that there shouldn’t be too many events on the same ticket, however “safe.” Of course, if the possible profit of the split ticket is not satisfactory for the player, they can increase its stake, at the cost of a higher possible loss.
The question arises as what would be a safety limit for the number of “sure” events on a ticket. There is not an absolute answer to this question, as it depends on everybody’s threshold of afforded risk and personal betting strategy. For evaluating the risk of any surprise occurring for the predictions of such a combined bet the only measure available is the overall payout odds, that is, the product of the payout odds of the constituent bets. A three-option bet (as it is that on final result 1X2 in matches) with payout odds between 2 – 3 for one option is usually categorized by the betting agencies as random, that is, any result is possible with about the same likelihood. Therefore, 2 as overall payout odds for a combined bet can be fairly chosen as a threshold for safety. This choice is also supported by the alternative of collapsing a combined bet into a different individual bet with the same payout odds, for the same stake: Instead of betting on a conjunction of several events, one may choose to bet the same amount on a single event with the same payout odds (as the product of the payout odds of the initially chosen combined bet).
In our example, instead of betting on the victory of the four favorite teams (with 1.2 payout odds each), one may choose a three-option individual bet of any kind with about 2 : 1 payout odds. In terms of house’s assessment, the two bets are relatively equally likely to be won. If you choose the individual bet as a result of personal analysis or using some objective information, the choice gets more justified. But even in the absence of such personal re-assessment of the chances for the individual bet, there is still an argument that inclines the balance toward the individual bet: House’s assessment is of course subject to error and approximation, even though it relies on statistical-mathematical algorithms (if it were not, there would be no surprises in the matches).
The likelihood of misestimating increases with the number of events considered and a misestimation for an “almost sure” event means overestimation for the chances of the (on-paper) favorite team. This statement is true also from the standpoint of the bettor – the more matches they analyze for predicting their results, the more likely is that they do it wrongly at some point. Doing it wrongly for only one event makes the combined bet loosing.
Conclusion
Overloading the betting tickets with several events thought as “almost sure”, for the sake of “safety”, is not a wise strategy. Such a combined bet might have decent payout odds, but the bettor might overestimate the chances that those events will happen together and as such, commit a conjunction fallacy. The more “almost sure” events on the ticket, the lower the chance to win.
The bettor actually chooses “safety,” but enlarging the number of bets on the ticket (with the purpose of having higher payout odds) actually reduces that safety. Of course, this behavior is in the advantage of the sports betting house.
A relatively safe strategy when betting on apparently “almost sure” events is to limit their number to have a maximum of about 2 overall payout odds, splitting the intended combined bet in this respect, or choosing an individual bet with the same payout odds for the same stake instead. Of course, the arguments do not apply for those bettors whose strategies are based on chasing surprises and the highest possible payout odds.
References:
Barboianu, C. (2022). Understanding Your Game: A Mathematician’s Advice for Rational and Safe Gambling. PhilScience Press.
Nilsson, H., & Andersson, P. (2010). Making the seemingly impossible appear possible: Effects of conjunction fallacies in evaluations of bets on football games. Journal of Economic Psychology, 31(2), 172-180.
Tversky, A., & Kahneman, D. (1983). Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment. Psychological review, 90(4), 293.



